How many sudoku puzzles are there?

I found myself wondering how many possible Sudoku puzzles there are, because, hey, that's the kind of thing I think about when there's nothing else for my brain to be doing. I went through a few approaches trying to figure out how to calculate it, and I'm not totally sure if the one I settled on is valid logic.

Consider a blank Sudoku puzzle:


Right now, with nothing determined, the upper left cell in the corner can be anything, so it has nine possible values. Let's write a nine there -- not representing that that's the value there, but that's the number of possible values that could be there.


Now let's assume we've figured out what the upper left cell is. That means there's eight possible values for the cell just right of it, and seven for the cell right of that, and six for the next one, and so on.


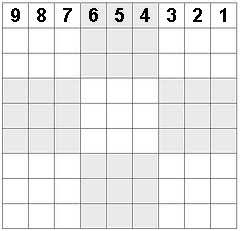
Following the same reason we can fill in more cells with how many possible values there are left for each one, based on the assumption that some valid value is in all the cells we've already filled in:

The order we fill in cells will decide what values end up in each cell, but I am fairly sure (though I probably couldn't prove it with mathematical rigor) that whatever order I choose, all the same values will end up in the grid, just in different places.

So far, I am nearly certain that I've proven something: if you multiply all the numbers written down so far, that's the total number of combinations of values that are possible in the cells that are filled in, in the set of all possible valid Sudoku solutions. (Right now, that's 407,586,816,000 possible grids.)

However, at this point it starts getting tricky. Consider the cell in row two, column four. We now know that three other cells in its row have been determined, and three other cells in its square. But we cannot conclude that that only leaves three possible values, since some of those might be the same. In fact, the same three numbers might appear in both groups, leaving six possible values here. But we can't just write in a six and proceed, because there are only six possible here in some of the 407,586,816,000. So we would need to figure out how many of those 407,586,816,000 have six, and how many have five, and how many have four, and how many have three; and then divide up the calculation. If we call those values N₆, N₅, N₄, and N₃, it would follow that N₆ + N₅ + N₄ + N₃ = 407,586,816,000. The total number of possible Sudoku puzzles with the cells filled in we have so far, and that next cell, would be equal to (6 * N₆) + (5 * N₅) + (4 * N₄) + (3 * N₃).

And once we try to do yet another cell, we will further have to bifurcate our calculation, including both those bifurcations, and the further bifurcations possible in that cell. Just a few more cells and this would go far beyond the bounds of calculability. Doing the entire puzzle would be impossible.

I've tried to come up with a different order to fill in the cells that would avoid this, and it's simply not possible. You can go back to the last version pictured above and try finding as many cells as possible you can fill in without a bifurcation, to minimize it. But more than half the puzzle will need bifurcations like this under the best of circumstances, where even three or four bifurcations makes the calculation impossible. So I must conclude my strategy is fundamentally unsound. It devolves into a brute force method too quickly.

The question I can't answer, though, is whether there is a more elegant solution. I suppose I should do a Google search to see who else has attacked the problem, but I'd rather give myself a few days to see if another idea occurs to me -- or if anyone posts some ideas on my comments.